Fast Fourier TransformIn this article, I talk about Fast Fourier Transform (FFT) which I used for arbitrary precision multiplication. I will also mention FFT multiplication for arbitrary precision arithmetic, later.
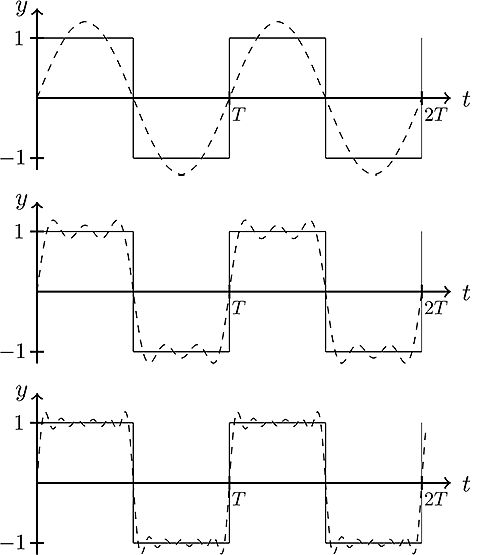
At first, I would like to start with “Fourier Series” which makes Joseph Fourier popular. “Fourier Series” is sum of sines and cosines which is expansion of a periodic function. Briefly, sum of sines and cosines represents a function or approximate.
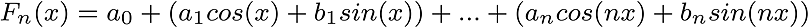
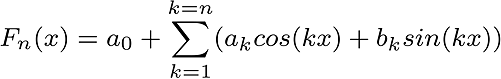
 a0, ai ve bi constants are coefficients of Fn(x).
Square Wave approximation with Fourier series,
a0, ai ve bi constants are coefficients of Fn(x).
Square Wave approximation with Fourier series,
 Periodic functions are represented with sum of complex exponentials. When we look at exponential functions, we see Euler’s number (e)
Recall; e constant
Periodic functions are represented with sum of complex exponentials. When we look at exponential functions, we see Euler’s number (e)
Recall; e constant
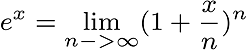
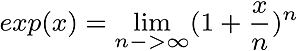
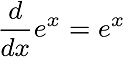 At this point, we see Euler’s formula. He discovered the relation between exponential function and trigonometric function.
At this point, we see Euler’s formula. He discovered the relation between exponential function and trigonometric function.
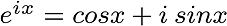
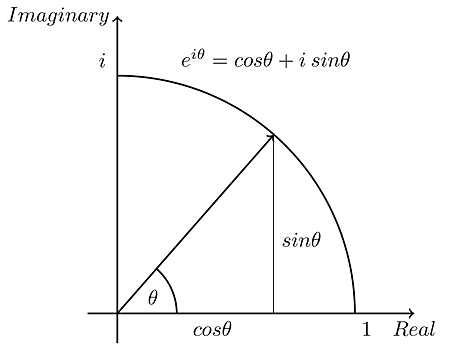 Recall; complex number
Recall; complex number
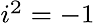 As is known, π radians equals to 180 degrees. So, if we put π, we see that
As is known, π radians equals to 180 degrees. So, if we put π, we see that 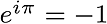 Because,
cos(π)=-1 and sin(π)=0
Complex numbers are represented with x, y on 2D coordinate system and π = 180 radians, cos(π) + isin(π) = -1
So,
Because,
cos(π)=-1 and sin(π)=0
Complex numbers are represented with x, y on 2D coordinate system and π = 180 radians, cos(π) + isin(π) = -1
So, 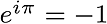 Now, if we focus on FFT, we see that integrable aperiodic functions are transformable with general Fourier Series formula, too. Time - frequency transformation is done at this point.
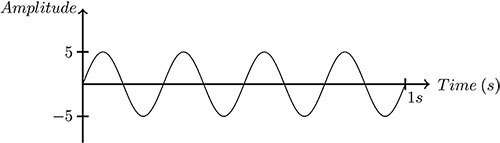
Time Domain
Now, if we focus on FFT, we see that integrable aperiodic functions are transformable with general Fourier Series formula, too. Time - frequency transformation is done at this point.
Time Domain
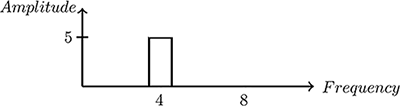
 Frequency Domain
Frequency Domain
 The FFT transformation.
The FFT transformation.
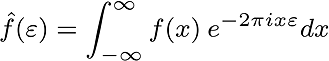 FFT Inversion is similar. (Be careful about the sign.)
FFT Inversion is similar. (Be careful about the sign.)
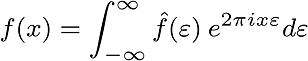 But, these functions are continuous and we must use discrete version of FFT in the digital world.
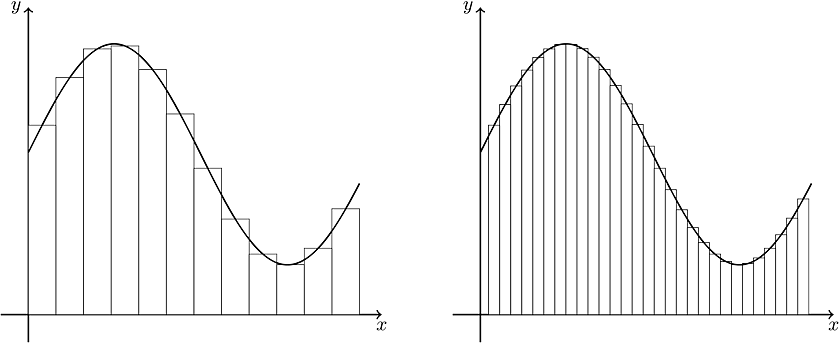
When we focus on Discrete FFT, we see Riemann's Sum Approximation which is a familiar method to be used for integration in digital world. As you see, if we draw more rectangles, we get more accurate results.
But, these functions are continuous and we must use discrete version of FFT in the digital world.
When we focus on Discrete FFT, we see Riemann's Sum Approximation which is a familiar method to be used for integration in digital world. As you see, if we draw more rectangles, we get more accurate results.
 and Discrete FFT is seen in this form,
and Discrete FFT is seen in this form,
 , n complex number array is transformed by DFT. , n complex number array is transformed by DFT.
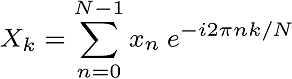 As an output, we get N-periodic complex number array.
As an output, we get N-periodic complex number array.
 Also, inverse of this operation is similar.
Also, inverse of this operation is similar.
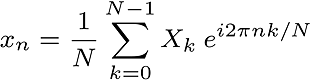 There is something that needs to be added. DFT algorithm's complexity is O(n²) and this means; the number of steps to do this operation, grows exponentially. So, we have to optimize it as much as possible(if we can). We may spend hours/days for an operation which can be done in minutes.
There is something that needs to be added. DFT algorithm's complexity is O(n²) and this means; the number of steps to do this operation, grows exponentially. So, we have to optimize it as much as possible(if we can). We may spend hours/days for an operation which can be done in minutes.
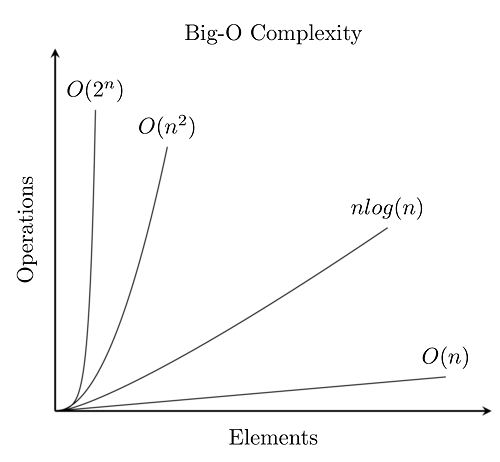 Fast Fourier Transform was developed for this reason and its complexity is O(nlogn). It brings significant time savings.
Divide and conquer philosophy lies behind it. The problem is divided into sub problems, solved recursively.
In this part, I shall mention about Cooley-Tukey FFT (Radix-2 Decimation-in-Time ) algorithm.
At first, we calculate odd and even indexed elements, separately and then bring together them again.
Fast Fourier Transform was developed for this reason and its complexity is O(nlogn). It brings significant time savings.
Divide and conquer philosophy lies behind it. The problem is divided into sub problems, solved recursively.
In this part, I shall mention about Cooley-Tukey FFT (Radix-2 Decimation-in-Time ) algorithm.
At first, we calculate odd and even indexed elements, separately and then bring together them again.
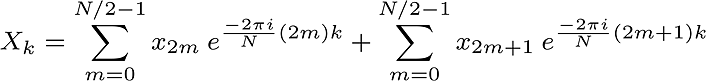 As you see, 2m represents even and 2m+1 represents odd index.
And we don’t do the same operations thanks to symmetry property of DFT.
In detailed form,
As you see, 2m represents even and 2m+1 represents odd index.
And we don’t do the same operations thanks to symmetry property of DFT.
In detailed form,
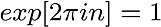 and
and
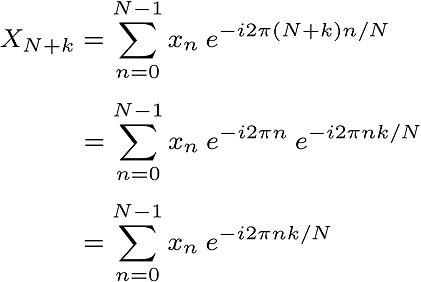
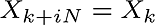 As you see, there is symmetry property. So, there is a common factor.
As you see, there is symmetry property. So, there is a common factor.
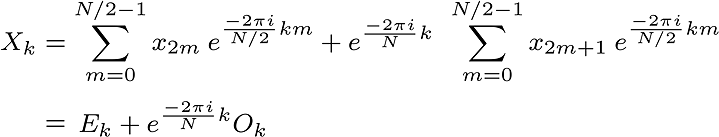 Taking into account that the DFT is periodic,
Taking into account that the DFT is periodic,
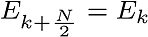
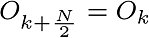 Finally,
Finally,
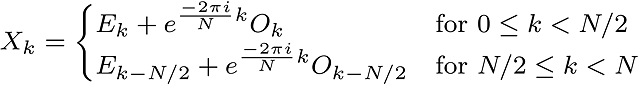 |

